ფიბონაჩის რიცხვები, ფიბონაჩის კოეფიცენტები, ფიბონაჩის ხაზები, ფიბონაჩის რკალები, ფიბონაჩის დროის სარტყლები (ზონები)

1,090 ნახვა

სარჩევი

ფიბონაჩის რიცხვები, ფიბონაჩის კოეფიცენტები, ფიბონაჩის ხაზები, ფიბონაჩის რკალები, ფიბონაჩის დროის სარტყლები – საბირჟო საქმიანობაში ყველაზე საიდუმლოებით მოცული და საინტერესო ცნებებია. მიუხედავად პროცესების მოჩვენებითი ქაოტურობისა, რომელიც ბუნებაში არსებობს, მათში შესაძლებელია გამოვავლინოთ კანონზომიერებებიც.

ასეთი კანონზომიერებების ერთ-ერთი მაგალითია ფრაქტალური გეომეტრიიის თვითმსგავსების პრინციპი (როდესაც ცალკეული ნაწილები მთლიანი ობიექტის მსგავსნი არიან) – ამის შესახებ ვისაუბრეთ, როდესაც განვიხილეთ ბილ უილიამსის ფრაქტალები. კიდევ ერთ საინტერესო კანონზომიერებაა – ოქროს კვეთა.

ოქროს კვეთა

არის მონაკვეთის ორ ნაწილად ისეთი დაყოფა, როდესაც მოკლე ნაწილის თანაფარდობა დიდ ნაწილთან, დიდი ნაწილის მთლიან მონაკვეთთან თანაფარდობის ტოლია. ქვედა სურათს თუ შევხედავთ, მაშინ ოქროს კვეთის შემთხვევაში a/b = b/c (სადაც c = a + b).

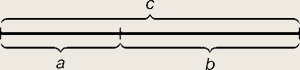
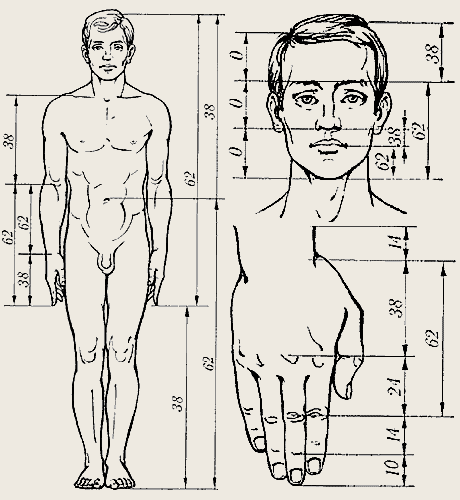
თვით წილადის სიდიდე გმოიხატება ირაციონალური სიდიდით, რომელიც დამრგვალებით 0.618-ის ტოლია. თუ განვიხილავთ ერთეული სიგრძის მონაკვეთს, მაშინ ოქროს კვეთა ყოფს მას ნაწილებად შესაბამისი ზომებით – 0.618 და 0.382. ოქროს კვეთა აღმოჩენილია ბერძენი ფილოსოფოსისა და მათემატიკოსის პითაგორას მიერ, ჩვენს წელთ აღრიცხვამდე მე-6 საუკუნეში. ბუნებაში ცოცხალი ფორმების დიდი რაოდენობა ოქროს კვეთში გამოისახებიან, მათ შორის ადამიანის ტანიც. მაგალითად მანძილი ტერფებიდან დაშვებული ხელების ხელის თითების ბოლოებამდე და მანძილი ამავე თითების ბოლოებიდან თავის გვირგვინამდე არის ზემოთ აღწერილი პროპორცოოს ფარგლებში. გარდა ამისა ადამიანის სახეზე და ხელის გულებზე ოქროს კვეთის მრავალი მაგალითია – დააკვირდით სურათს.

მიჩნეულია, რომ მოცემული რიცხვები “მაგიურ” კოეფიცენტებსაც წარმოადგენენ. ფიბონაჩის რიცხვების თანამიმდევრობა, რომელსაც სახელად მისი აღმომჩენის, იტალიელი მათემატიკოსის, პიზის მკვიდრის ლეონარდოს, რომელიც უფრო ცნობილია, როგორც ფიბონაჩი (ფინაჩის ძე) ეწოდა. ფიბონაჩის რიცხვები წარმოადგენენ ნატურალური რიცხვების თანამიმდევრობას, რომელშიც ყოველი მომდევნო რიცხვი ტოლია, ორი უკანა რიცხვის ჯამისა (თანამიმდევრობის პირველი ორი წევრი უდრის 1). ამგვარად, როდესაც ვსაუბრობთ ფიბონაჩის რიცხვებზე, ჩვენ ვგულისხმობთ თანამიმდევრობას: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 და ა. შ.

ფიბინაჩის კოეფიცენტი

არის ფიბონაჩის თანამიმდევრობის წევრების სხვადასხვა კომბინაციების ზღვარი. უკანა რიცხვის თანაფარდობის ზღვარი მიმდევნო რიცხვთან, ჩვენს მიერ განხილული ოქროს კვეთის წილადის 0.618-ის ტოლია. უკანა რიცხვის თანაფარდობის ზღვარი ერთ-ერთ მომდევნო რიცხვთან ტოლია 0.382-ის (რაც თავის მხრივ არის 1 – 0.618 სხაობის მნიშვნელობა). მომდენო რიცხვის თანაფარდობის ზღვარი, ფიბონაჩის თანამიმდევრობის უკანა რიცხვთან მიისწრაფის 1.618-სთან (მიაქციეთ ყურადღება რიცხვის წილად ნაწილს). მომდევნო რიცხვის თანაფარდობის ზღვარი ერთ-ერთ უკანა რიცხვთან მიისწრაფის 2.618-სთან (კვლავ მიაქციეთ ყურადღება რიცხვის წილად ნაწილს). ავიყვანოთ 1.618 კვადრატში და ჩვენ მივიღებთ რიცხვს, რომელიც ახლოსაა 2.618-თან. თუ ჩვენ ავიყვანთ მას კუბში, მაშინ მივიღებთ რიცხვს, რომელიც ახლოსაა კიდევ ერთ ფიბონაჩის კოეფიცენტთან – მომდევნო რიცხვის თანაფარდობის ზღვარის მაჩვენებელთან უკანა რიცხვამდე მეორე რიცხვთან (4.236). ასეთ არითმეტიკულ დამთხვევებს – რიცხვების მაგიას უწოდებენ.

ჩვენ ჩამოვყალიბდით ფიბონაჩის ძირითადი კოეფიცენტების განსაზღვრაში. ესენია – 0.382, 0.618, 1.618, 2.618 და 4.236. თუ ეს რიცხვები ასე კარგად გამოხატავენ ცოცხალი სამყაროს პროპორციებს, რატომ არ უნდა ვიპოვოთ მათი კავშირები პროცესებთან, რომლებიც ფინანსურ ბაზრებზე მიმდინარეობს? ასეც მოხდა. ფიბონაჩის თანამიმდევრობას დაემატა კიდევ ორი საკვანძო კოეფიცენტი 0.5 და 1 – და ფიბონაჩის კოეფიცენტების ასეთ კომპლექტს შევხვდებით შესაბამის გრაფიკულ ინსტრუმენტში, რომელიც ჩატვირთულია ფინანსური ბაზრების ანალიზის პრაქტიკულად ყველა პროგრამაში.

ფიბონაჩის ხაზები

ყველაზე მარტივ გრაფიკულ ინსტრუმენტად ითვლება. მათი აგების პრინციპი მარტივია. ტრეიდერი, ფასთა გრაფიკზე განსაზღვრავს ორ ათვლის (საყრდენ) დონეს (წერტილს), რომელთაგანაც ერთი შეესაბამება 100%-ს, ხოლო მეორე 0%-ს. მათ შორის ფიბონაჩის კოეფიცენტის პროპორციებში აიგება ჰორიზონტალური ხაზები (ხაზები, რომელთა კოეფიცენტი 100%-ზე მეტია, აიგება აღნიშნული დონეების გარეთ). ხაზების მაჩვენებლები აღინიშნება პროცენტებში: 38.2%, 50%, 61.8%, 100%, 161.8%, 261.8%, 423.6%. გრაფიკული ინსტრუმენტის აგების საკვანძო მომენტია ათვლის წერტილების მოძებნა. ითვლება, რომ ამ მიზნისათვის საჭიროა ავიღოთ ფასთა გრაფიკის საკვანძო ექსტრემუმები – წინააღმდეგობისა და მხარდაჭერის მნიშვნელოვანი დონეები. ანუ საყრდენი ხაზები უნდა დადგეს, ჩამოყალიბებულ საკვანძო მაქსიმუმსა (100%) და განვლილ საკვანძო მინიმუმს შორის (0%) – აღმავალი ტრენდის (ანუ ხარების ბაზარზე) დროს. ხოლო დაღმავალი ტრენდისას (ანუ დათვების ბაზარზე) პირიქით.

კლასიკური თეორიის თანახმად, ფიბონაჩის ხაზებმა უნდა გვიჩვენონ მხარდაჭერისა და წინააღმდეგობის მომავალი დონეები (ძლიერი ტრენდის დროს მაკორექტირებელი მოძრაობის დასასრული და ძირითადი ტრენდი გაგრძელება). არსებობს ფიბონაჩის ხაზების პრინციპების მრავალნაირი ინტერპრეტაცია, და მათ საფუძველზე სავაჭრო სიგნალების ფორმირების სისტემები. მათ განვიხილავთ საიტის სხვა სტატიებში.

ფიბონაჩის ხაზების გრაფიკული მაგალითი

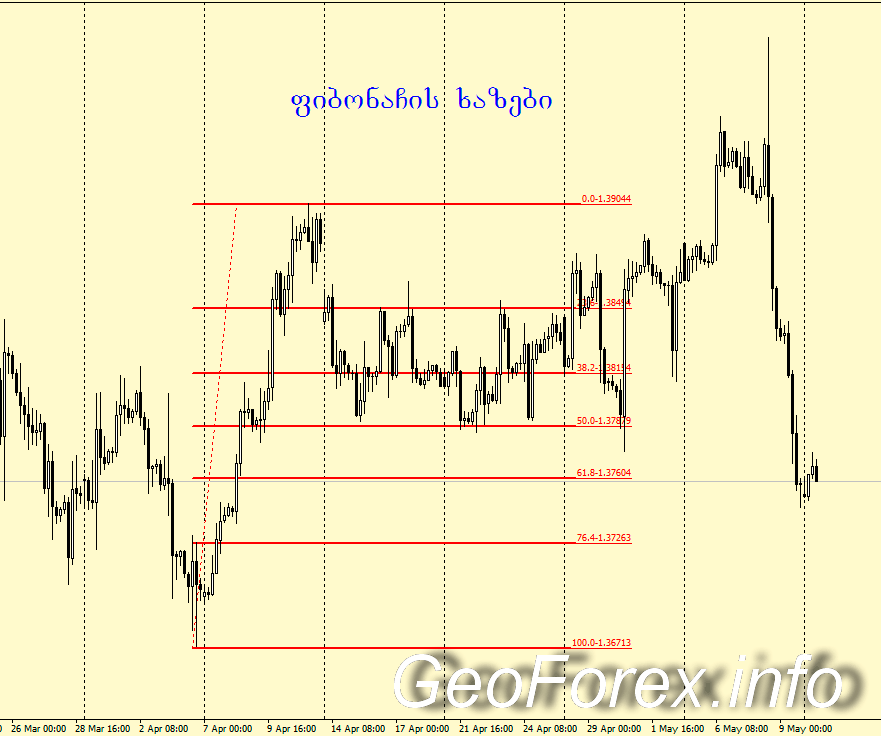
სურათიდან ჩანს, რომ დაღმავალი ტრენდის დროს (დათვების ბაზარი), ფიბონაჩის ხაზების შესაბამისი წესით აგების შემთხვევაში, ანუ სწორი საყრდენი დონეების მოძებნის შემთხვევაში, ჩვენ მივიღებთ წინააღმდეგობის დონეს 61.8%-ზე. შესამჩნევია, რომ 161.8% დონეც ასევე მნიშვნელოვანი წინააღმდეგობის დონე გახდება მომავალში. ასეთი კავშირების დანახვა ხშირად არის შესაძლებელი ისტორიულ გრაფიკებზე, მაგრამ რეალურ დროში, სავაჭრო გადაწყვეტილების მიღებისათვის ფიბონაჩის ხაზების გამოყენება საკმაოდ რთული ამოცანაა. ვინც ამ საკითხში კარგად გაერკვევა, ვაჭრობის წარმატებულობის მესამედი გარანტირებული აქვს.

ფიბონაჩის მარაო

კიდევ ერთ გრაფიკულ ინსტრუმენტს წარმოადგენს. მისი აგებისათვის საჭიროა გრაფიკზე ორი წერტილის მოძებნა – როგორც წესი გამოიყენება მნიშვნელოვანი ფასური ექსტრემუმები. პირველი წერტილი გვაძლევს მარაოს საძირკველს, ხოლო მეორე წერტილი, წარმოსახვითი მართკუთხა სამკუთხედის აგების დასრულების საშუალებას. ასეთი სამკუთხედის სიმაღლის ხაზი იყოფა ფიბონაჩის კოეფიცენტების პროპორციებად, რომელიც ქმნის მონაკვეთებს. სწორედ ამ მონაკვეთების საზღვრებზე გადიან ფიბონაჩის მარაოს სხივები. ფიბონაჩის მარაოს აგების მოჩვენებითი ჩახლართულობის მიუხედავად, იგი საკმარისად ტრივიალურია. მარაოს სხივები (თეორიაში) შესაძლკებელია მომავალში მოგვევლინოს წინააღმდეგობის ან მხარდაჭერის ხაზებად.

ფიბონაჩის მარაოს გრაფიკული მაგალითი

ფიბინაჩის რკალები

ფიბონაჩის ჯგუფის ინსტრუმენტებს შორის, საკმაოდ ფართოდ გამოიყენება. ისინი (რკალები) შემდეგნაირად აიგება. ისევე, როგორც მარაოს შემთხვევაში უნდა შეირჩეს ორი ექსტრემალური წერტილი, რომელთა შორისაც შესაძლებელია სწორი ხაზის გავლება. (საყრდენი ხაზის), რომელიც განსაზღვრავს ტრენდს (არ აგვერიოს ტრენდის ხაზში). მეორე წერტილი არის დასახაზი ელიფსის ცენტრი. ელიფსის ერთ-ერთი რადიუსი განისაზღვრება პირობით, რომლის მიხედვითაც ელიფსი უნდა გადიოდეს საყრდენი ხაზის პირველი წერტილზე.

ელიფსის მეორე რადიუსი – ემპირიულია, დგინდება ტერმინალის შემქმნელების მიერ და როგორც წესი მისი შეცვლა შესაძლებელია გრაფიკული ინსტრუმენტების პარამეტრებიდან. სავაჭრო ტერმინალში MetaTrader4, ფიბონაჩის რკალის პარამეტრი “მასშტაბი”-ს მნიშვნელობის დაყენება 10.0, ელიფსს გამოსახავს, როგორც წრეს. სტანდარტულ მნიშვნელობად გამოიყენება 1.0, რაც გამოიწვევს ელიფსის გაწელვას ჰორიზონტალური ხაზის გასწვრივ.

ფიბინაჩის რკალების გრაფიკული მაგალითი

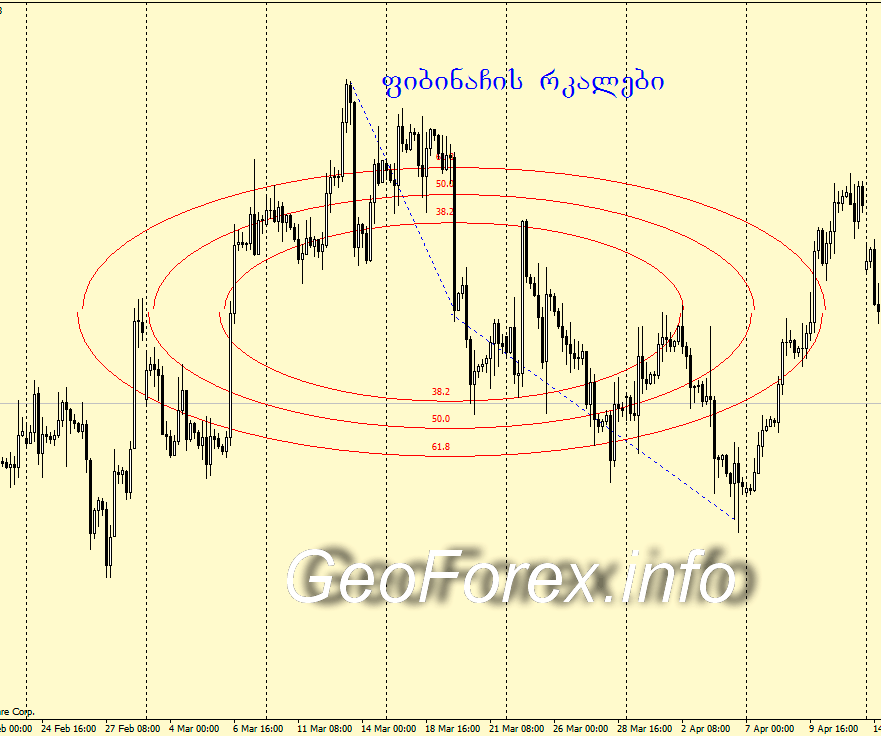
აღწერილი პრინციპით აიგება არა ერთი, არამედ რამდენიმე ელიფსი ერთდროულად. სხვა დამატებითი ელიფსების აგებისათვის, საყრდენი ხაზი (რომელიც აერთებს ორ ექსტრემუმს) იყოფა ფიბონაჩის კოეფიცენტების მიხედვით მონაკვეთებად, რომლებიც იწყება ელიფსის ცენტრიდან (მეორე წერტილი). ასეთი მონაკვეთების საზღვრებზე გადიან დამატებითი ელიფსები. როგორც წესი, გრაფიკული ინსტრუმენტი – ფიბონაჩის რკალები, გრაფიკზე ხაზავენ მხოლოდ ნახევარ ელიფსებს (ზედა ნახევარს მინიმალურ საყრდენ ხაზზე და ქვედა ნახევარს მაქსიმალურ საყრდენ ხაზზე), რის გამოც ინსტრუმენტმა მიიღო თვისი დასახელება – რკალები. რკალები (თეორიის მიხედვით) არიან მომავალი მხარდაჭერისა და წინააღმდეგობის დონეების მაჩვენებლები. როგორც წესი, ფიბონაჩის რკალებს გამოიყენებენ ფიბონაჩის მარაოსთან ერთად.

ანალიზისადმი ასეთი მიდგომის შემთხვევაში, წინააღმდეგობისა და მხარდაჭერის დონეებად განისაზღვრება რკალებისა და მარაოს სხივების გადაკვეთის წერტილები.

ფიბონაჩის დროის ზონები (სარტყელები)

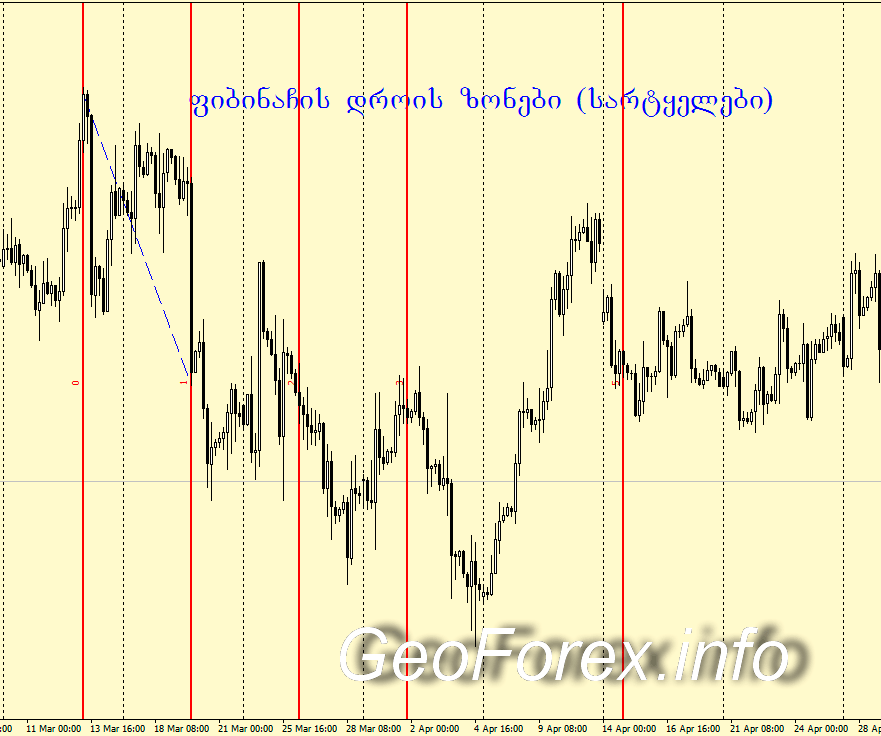
ბოლო გრაფიკული ინსტრუმენტია, რომელსაც ამ სტატიაში განვიხილავთ. მათი აგებისათვის ფიბონაჩის კოეფიცენტები არ გამოიყენება, სამაგიეროდ გამოიყენება თვით “მაგიური თანამიმდევრობის” რიცხვები. ფიბონაჩის დროის ზონების გრაფიკზე ასაგებად, ტრეიდერი თავისი შეხედულებისამებრ აძლევს ინსტრუმენტს, დროის მონაკვეთის მნიშვნელობას (მაგალითად, რომელიც შეესაბამება ფასის მნიშვნელოვანი მოძრაობის პერიოდს), რომელიც ჩაითვლება ერთეულად. მოცემული ინტერვალიდან მარჯვნივ აიგება დროის მონაკვეთები, რომელთა სიდიდე შეესაბამება 1, 1, 2, 3, 5, 8, 13 და ა.შ. მაჩვენებელს აღებულს თავდაპირველი პარამეტრისგან. ითვლება, რომ ასეთი მონაკვეთები შეესაბამება მომავალ მნიშვნელოვან ფასურ რყევებს.

ფიბონაჩის დროის ზონების გრაფიკული მაგალითი

ჩვენს მიერ განხილული იქნა ფიბონაჩის რიცხვები, კოეფიცენტები, ხაზები, რკალების და დროის ზონები. ჩვენ აქცენტი გავაკეთეთ იმ ფაქტზე, რომ ფიბონაჩის კოეფიცენტის “დანახვა” შესაძლებელია მრავალ ბუნებრივ პროცესებში. არსებობს თეორია, რომმლის მიხედვითაც ფინანსური ბაზრების გაანალიზება შესაძლებელია ფიბონაჩის გრაფიკული ინსტრუმენტების გამოყენებით. ამ თეორიის მეცნიერული ახსნა არ არსებობს. იგი ეყრდნობა მხოლოდ პრაქტიკულ გამოცდილებას, ისტორიულ და ვაჭრობის რეალური დროის რეჟიმში ვაჭრობის მონაცემებს. თანაც, ყველა ტრეიდერს თავისი პრაქტიკული გამოცდილება აქვს.

იმისათვის რომ დარწმუნდეთ მართლა მუშაობს თუ არა საფინანსო, მათ შორის ფორექსის ბაზარზე, ფიბონაჩის კოეფიცენტები – არის ერთადერთი გზა, თავად უნდა ჩაატაროთ ისტორიული და ონლაინ დაკვირვებები და დაადასტუროთ ან უარყოთ ზემოთაღნიშნული თეორია. ჩემი აზრით კი ფიბონაჩის ინსტრუმენტები ძალიან კარგად მუშაობენ საფინანსო ბაზრებზე, რის შესახებაც სხვა სტატიებში ვისაუბრებთ.

ლოგიკურად არსებობს ერთი ახსნა იმისა, თუ რატომ მუშაობენ საფინანსო ბაზრებზე ფიბონაჩის ინსტრუმენტები (და სხვა მრავალი ტექნიკური ანალიზის ინდიკატორები). იმიტომ რომ, მთელი მსფლიოს მასშტაბით, ძალიან ბევრი ტრეიდერი გამოიყენებს მათ პრაქტიკული ვაჭრობის დროს, სავაჭრო სიგნალების მიღებისათვის. ანუ ბაზრის ქცევის ფსიქოლოგიაში ეს ინდიკატორები უკვე ჩადებულია, ამიტომაც მუშაობენ ისინი.

უნდა აღინიშნის, რომ მკაფიოდ ფორმალიზირებული ტექნუიკური ანალიზის ინდიკატორებისაგან განსხვავებით, რომელთაც საკუთარ თეორიაში აქვთ სავაჭრო სიგნალების მიღების მკაფიო მექანიზმი, ფიბონაჩის გრაფიკულ ინსტრუმენტებს არ გააჩნიათ გამოყენების მკაფიო სამოქმედო ინსტრუქცია. ისინი იძლევიან მხოლოდ ვარაუდებს, მომავალი წინააღმდეგობის ან მხარდაჭერის დონეების ან ხაზების შესახებ.

***

***

***

***

რეკომენდებული ფორექს ბროკერი.